RC滤波的数字实现

信号与系统里面对数字滤波器的设计方法提供了方法论的指引，但在实际应用是会感觉难以使用，或者陷入公式的推导中间而无法对方法的本质做到“掌握”。这里对模拟系统离散化的一种方法——数值积分法的工程应用做一个简单的总结，并以RC滤波的设计为例子进行理论推导。

数字应用中常常需要对输入信号进行滤波处理，而达到较为平稳的输出结果，比如AD采样数据，如果直接使用采样进来的数据可能会发现比较大的抖动，在一个平均值附近进行无规律的跳动，这种数据可能无法直接用到数字控制或者监控系统。按照模拟的方法一般是加上低通滤波器滤除高频信号，得到较为平稳的采样数据。通过一些数学推导可以将该模拟滤波器通过数字编程实现，这里主要使用比较常用的模拟离散化方法——数值积分法，对原理的推导可以参考信号与系统理论，我们只利用结果进行推导。

RC 滤波的模拟电路简图

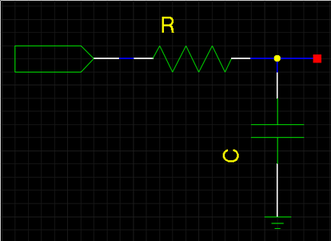
根据拉普拉斯变换可以得到RC系统的s域传递函数

\[Y(s)=X(s)\frac{\frac{1}{CS}}{R+\frac{1}{CS}}=X(s)\frac{1}{RCS+1}\]

通过数值积分法从s域变换为z域，其中T为采样频率

这里采用后向差法进行实例计算得到z域传递函数

\[Y(z)=\frac{X(z)}{RC \frac{1-z^{-1}}{T} + 1}\]

最后可以得到数字实现公式

\[y(n)=\frac{y(n-1)}{1+\frac{T}{RC}} + \frac{x(n)}{1+\frac{RC}{T}}\]

实际数字计算时为了简化计算过程，通常采样移位的方式替代乘除法，因此需要取2^k为计算步长，因此取 \(1+\frac{RC}{T}=2^k\) ，得到最后的计算公式

\[y(n)=(1-\frac{1}{2^k})y(n-1)+\frac{1}{2^k}x(n)\]

对应通用公式为

\[y(n)=(1-\alpha)y(n-1)+\alpha x(n)\]

这样就可以通过简单的移位操作进行程序处理，得到滤波器的数字实现，编程简单实现如下：

int rc_filter(const int adc)
{
    const int shift = 4;
    static int adc_shift = adc;

    adc_shift = adc_shift - (adc_shift >> shift) + adc;
    return (adc_shift >> shift);
}

这样就通过很少的内存占用（adc_shift）实现深度为4的一阶RC滤波。

另一方面，由于RC滤波器的延时特性，可以实现对信号的延迟处理，比如 DRC 处理中的attack time, release time 就可以通过简单的 RC 参数实现，当然这也是从模拟 DRC中获取的等效数字实现。

对于 RC 电路，有一个时间常数

\[\tau=RC\]

对应到数字实现，时间常数 d，代表经过 d 个 samples，输出达到 36.8%(-3dB) 的位置。

\[\alpha=e^{-1/d}\]

对应的 -3dB 截至频率的关系为

\[\alpha=e^{-2\pi f_C}\]